O crochê e a matemática

"Matemática é uma linguagem que possui uma lógica interna. Mas o que é tão impressionante sobre essa linguagem é que ela parece descrever a maneira como o mundo funciona – não apenas às vezes, não apenas aproximadamente, mas invariavelmente, e com uma exatidão infalível." – John D. Barrow, em The Mathematical Universe

Por muito tempo só se conhecia dois tipos de geometria: a euclidiana e a esférica.
Euclidiana é a geometria mais popular, é a geometria dos quadrados, dos planos, dos ângulos retos, e a que se acredita que represente o próprio tecido do nosso universo. Mas não temos tanta certeza disso, porque é muito difícil medir com precisão o formato do universo, já que ele é imenso e nós só conseguimos medir uma minúscula parte. Seria como uma formiga tentar medir a curvatura do planeta Terra. O planeta vai parecer plano para ela, mas isso é só porque ela é muito pequena.
A geometria esférica é a das esferas.
No início do século dezenove foi comprovada, através de cálculos e deduções matemáticas, a existência de um terceiro tipo de geometria: a geometria hiperbólica. Um plano hiperbólico é como uma esfera ao contrário, no sentido de que não tem fim, não é fechado em si mesmo, e aumenta indefinidamente sua curvatura de forma exponencial.
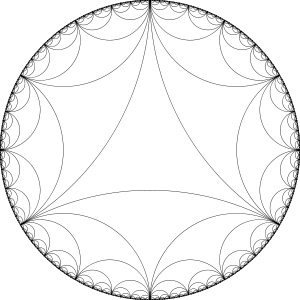
Por mais que todos os cálculos a comprovassem, a geometria hiperbólica ainda era totalmente difícil de imaginar. Suas representações normalmente eram assim:

Mas, em 1997, a professora de matemática Daina Taimina descobriu que existe, sim, uma maneira de se construir modelos de planos hiperbólicos no nosso mundo 3D, e é através da centenária arte do crochê. https://twitter.com/DainaTaimina

Extraído de: Como uma Delicada Forma de Artesanato Revolucionou Nossa Maneira de Perceber a Matemática, por Caroline Barrueco. In: Noosfera

Slideshow TRICOTANDO E CROCHETANDO